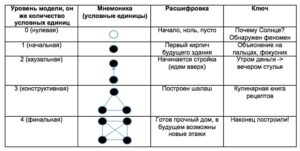
Вопросы, обнаружение феноменов, формирование понятий
Подробнее в статье: Фазы развития моделей

 0
0
В начале были «Начала». Сейчас поясню. Мы тут с Вами в прошлый раз обсуждали проблему осуществления переводов. Выяснили, что качество оных сильно разнится в зависимости от мастерства исполнителей. И я как-то запамятовал запустить свою любимую, хоть и уже несколько заезженную на страницах этого блога пластинку – о жгучих проблемах нашей национальной лингвистики. Теперь уж и не буду, дабы не портить никому настроение. Напротив, постараюсь его поднять, сообщив, что в отдельных случаях русскоязычные варианты некоторых названий значительно удачнее иностранных. В качестве примера приведу «Начала» Евклида. В греческом оригинале это были «Στοιχεῖα». Читается это на новогреческий манер почти как «Стихии», а дословно переводится как «Элементы». На латыни из этого получилось Elementorum, производные из которого уже впоследствии прониклив английский (Elements) и прочие европейские языки. И на русском первые Евклиды были «Елементами» и даже «Стихиями», однако почему-то прижились «Начала» с подачи Петрушевского. С моей точки зрения, это замечательный перевод, поскольку единое слово в нем несет на своих плечах одновременно два смысла. Дело в том, что эта книга, и в самом деле, была в начале славных дел – почти тех же самых, что имелись в виду в книге «Бытия» или Евангелии от Иоанна. На ее фундаменте было возведен не один корпус величественного здания современной науки. Она служила идеалом дедуктивного вывода для бесчисленного количества мыслителей. Она оказала существенное влияние на модели Коперника, Кеплера, Галилео, Ньютона. По ее образу и подобию построены философские труды Гоббса, Спинозы, Уайтхеда и Рассела. Ее можно считать почетным прародителем логики, математики и информатики. Это был исторически первый пример аксиоматической системы, наглядно показавший, какие неожиданные заключения можно произвести из простого набора незамысловатых постулатов. К счастью, далеко не последний…
Но еще задолго до «Начал» уже были числа. По мнению многих современных философов (и не менее современных физиков), адекватность применения математического аппарата к моделированию окружающего нас мира само по себе является загадочным феноменом, требующим объяснения. Но еще за многие века до наших дней Пифагор узрел числа повсюду вокруг себя и предположил, что именно они являются теми первичными кубиками, из которых построен весь космос. Может быть, не так уж и далек был он от истины?! Но еще за многие тысячелетия до Пифагора homo sapiens овладел приемами абстрактного мышления. С их помощью можно было отфильтровать то, что рознило объекты друг от друга, и затем, сгруппировав их, построить ментальную модель «единого» и «множественного». Отсюда был ровно один шаг по лестнице моделей к числам. Проще всего было определять количества на пальцах. Именно с их помощью подсчитывали немногие предметы своего (или чужого) обихода или немногих своих (или чужих) домашних животных наши далекие предки. Пальцев, как известно, пять на каждой руке, десять на двух. Если задействовать еще и нижние конечности, то получится двадцать. Последнее, вероятно, Вам покажется экзотикой, ведь на ногах считать как-то не с руки. Тем не менее, к этой системе независимым путем пришли народы различных культур, разделенные друг от друга гигантскими океанами, безводными пустынями или непроходимыми горами. Например, именно так считали индейцы майя и некоторые прото-европейцы. Рудименты сей примитивной бухгалтерской системы сохранились даже в современном французском языке. Например, число 84 – это «quatre-vingt-quatre», что в буквальном переводе означает «четырежды-двадцать-и-четыре».
Что же было еще раньше, до числа?! Конечно же, в еще более первоначальном начале было слово. Имеются в виду знаки, символы. Ведь даже многие виды животных имеют примитивные системы передачи информации друг другу. Коль скоро произносимые ими звуки или производимые ими телодвижения несут смысловую нагрузку, то каждая распознаваемая комбинация из них – модель чего-то (например, ситуации опасности). И эта способность быстро пригодилась людям в развитии технологии счета. В начале совершенно необходимо было придумать средства для репрезентации цифровой информации, т.е. знаки для ее сохранения и передачи. Изначально числа показалось удобным представлять в виде зарубок на каком-нибудь подходящем материале под руками, например, на обглоданных костях. Однако развитие жизни приносило с собой новые требования для систем исчисления. Что делать, если требуется записать очень большое число, превышающее набор щупальцев на теле человека? Одним из популярных решений стало введение в набор цифр дополнительных символов. Когда загибать становилось больше нечего, проставлялась особая метка. По понятным причинам это происходило каждые10 или 20 отсчетов. Непосредственным плюсом такой системы была относительная простота записи (и последующего плюсования) количеств. По другим критериям люди пришли к альтернативным базовым основаниям, среди которых выделялись 12 и 60. Почему именно эти числа? Возможно, что свою роль сыграло количество новолуний в году. Абсолютно точно, что важным фактором стало наличие у них множественных делителей. Наши далекие предки, в точности, как и некоторые двоечники начальных классов, недолюбливали дроби за сложность манипуляций с ними. Шестидесятеричная система была взята на вооружение в Вавилоне. С ее помощью удобно было фиксировать положения блуждающих звезд, крайне важных для произведения астрологических предсказаний. Широко известно, что именно из этого халдейского наследия мы почерпнули наше деление углов на градусы, а времени на часы, минуты и секунды.
Что же изменилось с началом эры Аббасидского халифата? Математика быстро попала в фокус внимания мусульманских ученых. Главный персонаж предыдущей статьи Хунайн ибн Исхак сделал уже третий (известный историкам) перевод «Начал» Евклида, значительно улучшив качество предыдущих. Но еще за сто лет до этого в Багдад были импортированы индийские цифры, которые мы теперь величаем арабскими. Наша десятичная система, где особое значение принимает местоположение (позиция) внутри числа (и тем самым является, как говорят математики, позиционной), впервые зарегистрирована в сочинении под названием Арьябхатия шестого века христианской эры. Спустя столетие появилась Сиддханта Брахмагупты, которая впоследствии (скорее всего еще при аль-Мансуре) была переведена на арабский язык (то ли напрямую из санскрита, то ли через персидский). Уже в славные для науки времена аль-Мамуна два почетных члена-корреспондента его Дома Мудрости — аль-Кинди и аль-Хорезми (мы посвятим их творчеству отдельные статьи) написали обширные комментарии об использовании новых индийских штучек. Переводы уже этих произведений на латынь внедрили эту прогрессивную арифметическую технологию в ментальные модели Западной Европы, откуда она в свое время проникла и в Россию. Произошло это, однако, далеко не сразу. Еще многие столетия (по крайней мере вплоть до восемнадцатого века) широко применялась римская нотация, которая, в свою очередь, происходила из древнегреческой, где для обозначения цифр пользовались буквами, фиксированные значения которых просто складывались друг с другом. Недостатки ее были постепенно осознаны учеными только по мере дальнейшего развития науки, поскольку алгоритмы произведения арифметических операций с закодированными с ее помощью числами (например, умножение или деление) были чересчур сложны. Помимо этого, новая система позволяла легко и относительно компактно записывать сколь угодно большие величины.
Ну, а что было в самом начале всех начал?! Скорее всего, «ничего» и было. Философское понятие совершенного отсутствия чего-либо можно при желании обнаружить в «Физике» Аристотеля. В истории же развития моделей чисел непустое место занимает 0. Аналоги наших нулей можно найти еще в Вавилонской клинописи, разве что они почему-то не любили помещать их в самый хвост. Догадываться, что именно имелось в виду (например, 10, 100 или 1000), предполагалось при помощи контекстной информации. Вполне возможно, что виновата в том была сама шестидесятеричная система – нулей в ней требуется намного меньше, чем в десятичной, поэтому и разборки с ними происходили значительно реже. Греки под вероятным влиянием этих товарищей с Востока использовали аналогичную систему для записи дробной части чисел. При этом так уж случилось, что для записи нулей ими был выбран похожий на современный символ «о» (греческая буква «омикрон»). Чем отличились в этом процессе интересующие нас арабы? Нет сомнений, что они получили «0» в качестве бесплатного довеска в общем пакете инноваций из Индии. Тем не менее из их творчества очевидно, что они долгое время относились к этой сущей безделице с подозрением. Положим, алгебраическое уравнение типа x2 + 2x – 15 = 0 записывалось ими исключительно в канонической форме x2 + 2x = 15.Однако четко прослеживается, по крайней мере, этимологическое наследие. Арабское слово «сифр» (означающее «ничто») неисповедимыми путями (через средневековую латынь) превратилось и в «цифру», и в «зеро» одновременно.
В чем же основной вклад исламской цивилизации в начало начал – развитие наших моделей чисел? Арабофилы увидят его во всем вышеперечисленном и добавят сюда еще изобретение методик работы с десятичными дробями. Арабофобы, в лучшем случае, определят его полезность исключительно как временное ответственное хранение чужих знаний. А я Вам вот как скажу. Сама постановка этого вопроса для нас малоинтересна, даже ошибочна. Это — типичный евроцентризм. Это – неадекватный в наших целях угол абстракции. Это – все равно, что видеть яблоню как аппарат для производства яблок, которые мы едим. Мы с Вами не имеем права определять ценность тех или иных персонажей в прошлом на основании того, как они (вероятно) каузально повлияли на кажущиеся нам прогрессивными преобразования в будущем. Такой подход хромает анахронизмом. Если же посмотреть на события глазами человека девятого века, то именно в Багдаде халифа аль-Мамуна человечество собирало силы для решительного броска через хребет Аристотеля к плодородной долине науки. Никакие боги еще не определили неизбежность провала этого предприятия. Оно могло быть успешным. Если оно таковым не стало, то на то должны существовать определенные причины. Наше с Вами дело, как историков моделей – постараться их локализовать и сделать адекватные выводы на будущее. На пути решения этой задачи давайте пока зарегистрируем факт заложения многочисленных начал и «Начал» в фундамент будущего модельного здания…
Не числами едиными жив математик. И не их репрезентацией. Надо еще овладеть искусством ими ловко манипулировать. Этот человек знал толк в жонглировании цифрами. Джордж Сартон именовал целую эпоху в честь этого человека. Но этот человек был вовсе не из Кемерово. Кто тогда это был и откуда? Об этом и о многом другом расскажет Вам Блог Георгия Борского.
Модели, предложенные в целях концептуализации исторических событий и оценки деятельности исторических личностей, являются интеллектуальной собственностью автора и могут отличаться от общепринятой трактовки.
«Познай самого себя» — говорили мудрые древние греки, но и современные авторитеты нисколько не сомневаются, что они были правы.
Уважаемые читатели, дорогие друзья! Пара слов о самом себе. Без малого четверть века тому назад я покинул свою историческую родину, бывшую страну коммунистов и комсомольцев и будущую страну буржуев и богомольцев.
Ну вот, мы и снова вместе! Надеюсь, что Вы помните — в прошлый раз я определил тематику своего блога как «История моделей».