Вопросы, обнаружение феноменов, формирование понятий
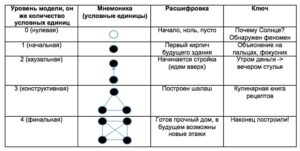
Подробнее в статье: Фазы развития моделей

 0
0
В начале были анекдоты на кухне. Отксеренный Солженицын, «Покаяние» и ГКЧП были потом. Насколько банальная болтовня оказалась эффективна в расшатывании могучего советского строя?
Можно ли вообще такими скромными средствами оспорить могущество правящих ментальных моделей? В начале у нас были просто смутные ощущения обмана — уж слишком приторно лубочную картинку рисовали учебники и показывал телевизор. Мы долго не верили этим чувствам, поскольку они противоречили всему, что мы выучили. Однако постепенно снежный ком неортодоксальных фактов нарастал и превращался в ледяной кулак. С его помощью мы разрушили гигантскую стену лжи и, счастливые открывшейся перспективой, немедленно начали возводить новую. А сейчас мы удивляемся тому, что когда-то позволяли себя так одурачить. В начале совсем другой истории был английский философ Джон Лукас. Именно ему принадлежит честь (или бесчестие?) исторически первой формулировки утверждения о «слабосильности ИИ», которое оказалось в фокусе нашего внимания в предыдущей статье. Если в четырех словах, то его можно сформулировать так: искусственный интеллект слабее естественного. Конечно же, не в манипуляциях с гигантскими цифрами или массивами данных, или любой другой легко алгоритмизируемой механической деятельности. Речь шла о тех задачах, которые принято величать креативными. А потом был Роджер Пенроуз, влиятельный ученый с мировым именем, который тоже решил подать свой голос в защиту этой модели. К моменту выхода его книги «The Emperor’s New Clothes» в большой тираж фанфары нашей прессы без устали трубили бессмертную славу грядущему царству роботов. Поэтому прозрачный намек на знаменитую сказку Ганса-Христиана Андерсена легко расшифровывался. В известном каждому с детства сюжете о прозрачном одеянии одного невзрачного монарха тоже была чисто эпистемологическая начинка. Чему следует верить – собственным глазам или признанным авторитетам?
Однако, в отличие от чудесной сказки, в нашей с Вами реальности от этого гласа народного из толпы решительно никто не прозрел. Напротив, на презренное разброд, шатание и болтание накинулась вся королевская рать. Что там скворчит этот глупый малец? Пусть это голая ложь, самодержца не трожь! Юную модель сбросили со стены, а осколки развеяли по ветру. Чтоб не пришлось самому кости собирать, еретик Пенроуз предпочел замолчать. Откуда столь непредвиденный классиками мировой литературы результат с одной стороны и такое верноподданническое рвение с другой? Дело в том, что сторонникам ортодоксии есть что терять, помимо своих цепей «сильного ИИ» (напомню, наша версия этой пропозиции несколько отличается от той, которую атаковал Джон Серл своей «Китайской комнатой»). Если верить тезису Черча-Тьюринга (а нет ни малейших оснований иметь сомнения на его счет), то при помощи наших компьютеров можно сделать абсолютно все, что в принципе вычислимо средствами нашего физического мира. Предположить, что жалкие двуногие и бесперые в состоянии перепрыгнуть через их теоретически известные ограничения (прежде всего, в решении комбинаторно сложных задач) – так и в пучине религиозного мракобесия можно сгинуть! Отступать просто некуда – за спиной господин великий физикализм-материализм.
Каковы же были основания для критики существующего строя? Роджер Пенроуз, будучи математиком, вслед за Джоном Лукасом замахнулся на строгое демонстративное доказательство своего утверждения. Однако сил чистой дедукции для импичмента безраздельно царствующей ментальной модели банально не хватило. Это было очевидно самому Пенроузу, который называл свое построение «спекулятивным», т.е. не претендующим на большее, чем муссирование мутных интуитивных ощущений лжи. Многочисленные критики обнаружили в цепи его рассуждений не менее многочисленные слабые звенья. С тех пор прошло без малого тридцать лет. Что изменилось с тех пор? Наш мир от этой эскапады ничуть не пошатнулся. Напротив, продолжил вращаться в выбранном направлении. Голый король стал уже, пожалуй, императором, городов и весей диктатором. Гигантские подати ему платят соединившиеся пролетарии и буржуи всех стран золотого миллиарда, многополярного мира черного золота и многие другие. Одни ожидают от него прорывов в еще более золотой век. Другие задрожали и упали в обморок, ожидая неминуемый апокалипсис. Однако, с моей точки зрения, партия Лукаса-Пенроуза еще отнюдь не проиграна, в их ментальной позиции наличествуют скрытые резервы. Сегодня я постараюсь не математикой, так философией внести свой скромный вклад в расшатывание неприступных бастионов моделей робототеистической ортодоксии. Кто-то всегда за тех, кто побеждает. А вот я всегда за тех, кого обижают. Типичная борьба Борского в стиле безнадежного оптимизма — мы пойдем другим, блоговым путем.
Каким именно? Сперва постараемся собрать Шалтая-Болтая из разбитой скорлупы, взболтаем старую болтушку. Обратим внимание на то, что тезис «слабосильности ИИ» можно (возможно, еще несколько слабее) переформулировать так: «Существует некая полезная деятельность, в которой человек может функционировать эффективнее, чем компьютер». Под «полезностью» здесь понимается нечто прагматически ценное относительно наших шкурных интересов. Этот предикат нужен для того, чтобы исключить, например, «нечестность». Люди в этом большие мастера, но сие достижение не делает им чести. Что же мы ценим больше всего? В данном когнитивном контексте, конечно же, знания. Ментальные модели сделали из обезьяны homo sapiens. Именно селекция самых адекватных из них – самое важное для нашего рода занятие. Итак, повестка дня принята, приступим к прениям. Для доказательства истинности вышеприведенного утверждения (благо оно экзистенциального типа) достаточно привести всего лишь один эмпирический пример. По моему убеждению, таковых на самом деле в истории моделей можно обнаружить великое множество.
Проблема заключается в том, что не так-то просто точно вычислить масштабность решенных человечеством творческих задач. Среди них, однако, есть одно важное исключение – шахматы. Как, скажете Вы, разве как раз эта игра не является прямым свидетельством обратного? Разве софт на мобильниках не даст фору большинству любителей? Разве сильные движки не обыгрывают чемпионов мира? Это и в самом деле так, что я вовсе и не собирался отрицать. Но я сегодня буду говорить об ином – не о сравнительной практической силе белковых и кремниевых шахматистов (т.е. об их умениях), а об их сравнительных способностях по познанию мира (т.е. по приобретению знаний). В данном случае по познанию микромира древней забавы королей. Как же устроить это состязание? Для начала представим себе, что шахматы изобрели ровно пять минут тому назад. То есть, у соперников нет совершенно никаких наработок, помимо правил. А теперь посмотрим, на что способны железные рыцари против беззащитных созданий, вооруженных одними голыми мозгами. На старт… Внимание… Часы запущены! Ваш ход, маэстро И.И.!
Голым перебором эту задачу не побороть. Шахматы – игра конечная, т.е., количество уникальных позиций в ней ограничено. Тем не менее их слишком много, больше, чем атомов во Вселенной. Если четырнадцать миллиардов компьютеров, работающих в четырнадцать миллиардов раз быстрее текущих, заставить считать четырнадцать миллиардов лет (прошедших с сотворения мира), то они с гигантским запасом не справятся. Можно, конечно, попробовать распутывать с самого конца – с максимально простых окончаний. Именно по этому принципу построены т.н. таблицы Налимова – на каждую позицию в них приведены лучшие ходы. Рассчитаны они в настоящее время вплоть до 7 фигур, а требуется 32, причем сложность задачи с добавлением каждой возрастает экспоненциально. Это когнитивный тупик, как из него выходить? Оказывается, есть и такая партия! Для этого достаточно сообразить, что вовсе не обязательно задавать пары <позиция x, оптимальный ход y> табличным образом (давайте назовем такой подход «экстенсиональным»). Если найти формулу-алгоритм, которая будет успешно делать из иксов игреки, то мы справимся с данной задачей значительно меньшими затратами (а этот путь будет у нас «интенсиональным»). Но где же зарыта искомая функция?
Почти на поверхности нашего головного мозга, если пользоваться нейронными сетями. Честно говоря, как в точности работает биологическая разновидность оных, до конца неизвестно. Зато их математические модели хорошо изучены. По существу, они представляют собой такой универсальный преобразователь входов в выходы, который посредством подбора набора коэффициентов может аппроксимировать произвольную кривую. На самом деле, почти произвольную. Предположим, что наша кривая на самом деле является прямой. Тогда для ее реконструкции достаточно всего лишь двух параметров – угла наклона и смещения. Однако это случай вырожденный. Если она не окажется достаточно «гладкой», то и настраиваемых параметров потребуется ничуть не меньше, чем строк в таблице Налимова. Обладает ли идеальный шахматный алгоритм таким атрибутом «гладкости» — вопрос, конечно, интересный, но полностью нерелевантный тому, что мы желаем от него получить. Прошедшая полный курс обучения нейронная сеть, может быть, и будет безумно сильно играть, но при этом окажется «непрозрачной» для ума. Она не будет содержать того, что мы хотели раздобыть — «знания». Другими словами, ее турнирные успехи будет невозможно сохранить, передать другим и, тем более, перенести в другой домен. Коль скоро цель нашего интеллектуального занятия «полезность», то и это путь в никуда. А ведь именно по этому пути пошли все наши лучшие шахматные движки, не сделав ни малейшего вклада в теорию игры.
Позвольте, но ведь люди ее как-то создали? Означает ли эта фундаментальную шаткость позиций «сильного ИИ»? Не прав ли тогда был Пенроуз, когда заявлял: «[У меня есть] чувство “очевидности” того, что, хотя многое из происходящего в ментальной деятельности могло бы работать как компьютер, сознательный разум в целом не является таковым». Увы, это всего лишь показания детектора лжи внутри него. Да и то рассуждение, которое мы привели до сих пор, не может считаться даже доводом ни в пользу «очевидности» этого чувства, ни в пользу нашей версии тезиса «слабосильного ИИ». Необходимо сначала доказать, что созданная шахматистами теория была чем-то «полезным». А затем еще и показать, что не существует другого способа достичь того же самого алгоритмическим путем. Мало самому увидеть голого короля, надо еще доказать всему миру его наготу, подчеркнув его отличие с модно одетой моделью. Поэтому статус всего, что было сказано до сих пор, пока не выше, чем типичная блоговая болтовня. Но это была только присказка. Настоящее шатание основ будет впереди…
Итак, наша дуэль с «сильным ИИ» хоть и состоялась, но снова перенесена. Партия откладывается. В позиции белых налицо некоторый кризис жанра. Срочно требуются свежие идеи. Самое время заглянуть за плечо человеческому Е.И. Как он решал проблему приобретения знаний? Идет охота на голого короля – в Блоге Георгия Борского.
«Познай самого себя» — говорили мудрые древние греки, но и современные авторитеты нисколько не сомневаются, что они были правы.
Уважаемые читатели, дорогие друзья! Пара слов о самом себе. Без малого четверть века тому назад я покинул свою историческую родину, бывшую страну коммунистов и комсомольцев и будущую страну буржуев и богомольцев.
Ну вот, мы и снова вместе! Надеюсь, что Вы помните — в прошлый раз я определил тематику своего блога как «История моделей».