№393. Чуднóе чудо

Задача задаче рознь. Эта элементарная моделька, знакомая каждому первоклашке, научившемуся отличать «двойку» от «пятерки» и «на раз-два» от «хоть убей», давно развита математиками в могучую теорию вычислительной сложности. Стройная иерархия, насчитывающая десятки — пожалуй, уже сотни — различных классов, постоянно растущее множество лемм и теорем, тем не менее, не оказывают должного влияния на ход мышления сторонников гипотезы т.н. сильного искусственного интеллекта. Из того, что Ваш калькулятор с легкостью жонглирует гигантскими числами, а мобильник обыгрывает Вас в шахматы, логически не следует то, что робот когда-либо станет чемпионом мира в странную игру по имени жизнь. Сей вывод – ложь, многократно повторяемая и потому все более смахивающая на истину, типичная ошибка индукции. Но что еще хуже того – весьма вероятно, что традиционному компьютеру не стоит и замахиваться на эту задачу. И причина тому проста – она принадлежит принципиально другому классу сложности. Да что там жизнь! Возьмем хотя бы те же шахматы, как я это некогда сделал ранее, и рассмотрим вместо традиционной проблемы «найди сильный ход», отлавливаемой в банальные нейронные сети, казалось бы, ее ближайшую соседку по 64-м клеткам: «почему найденный ход сильный?» Представьте себе, в общем невырожденном случае, вместо спокойно проходимой за т.н. полиномиальное, т.е. приемлемое время дороги, мы попали с Вами в непроходимые джунгли категории NP-hard, а в определенной формулировке и EXP-hard (т.е. со сложностью, растущей экспоненциально вместе со входными данными). Тем не менее, при астрономических размерах фазового пространства возможных позиций, наши с Вами сородичи, простые двуногие и бесперые смертные, пусть и обладающие горделивым званием мастеров или гроссмейстеров, но не имеющие полупроводникового быстродействия в мозгах, замечательно с ней справились. Причем, сравнительно небольшим творческим коллективом в несколько тысяч человек за смешные по расчетным меркам считанные десятилетия.

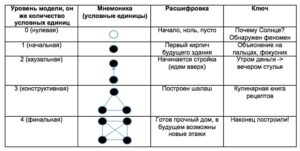
Что же делает эту задачу столь особенной? Дело в том, что здесь речь идет об открытии законов природы Вселенной, но не нашей, а той, что зовется «шахматы». Требуется ведь не только выиграть, а понять причину произошедшего и сделать корректное, релевантное обобщение, вербализировав его по дороге. Другими, нашими словами, создать модель. Результирующая рекомендация, в некотором отличие от физических формул, получается не слишком точной, типа ceteris paribus (при прочих равных) – т.е. правила, из которого существует множество исключений. Тем не менее, нетрудно продемонстрировать, что она весьма полезна на практике. Как автоматизировать этот процесс? Последовательной генерацией адекватных гипотез и последующей проверкой их на сгенерированных эмпирических данных, в данном случае, партиях – по-иному никак не получится, поскольку фазовое пространство чересчур негладкое, скалистое. Беда в том, что этих гипотез экспоненциально много, а с вычислением предиката адекватности-релевантности дело и вовсе труба – углы в непроходимых джунглях никакими алгоритмами не срезать. Несложно подметить фамильное сходство вышеописанной процедуры с другим популярным занятием человека разумного – наукой. И впрямь, деятельность ученых весьма похожа на работу шахматных теоретиков, разве что она еще более трудоемка, поскольку значительно объемнее, да и наполнение базы фактов сопряжено с серьезными практическими затруднениями. И опять хуже того – прежде, чем проверять любую гипотезу, требуется догадаться, какую именно следует выдвинуть. Для этого в свою очередь необходимо первоначально определиться с тем, какие именно факторы являются в данном случае релевантными и адекватными для предполагаемо каузально зависимой переменной. Но в самом-самом начале начал придется решить какой именно феномен нас интересует, какие именно вопросы по этому поводу будем задавать и в терминах каких именно понятий будем их исследовать. Успешно пройти одну эту, т.н. нулевую фазу развития менталки, по крайней мере, экспоненциально сложно. Сегодня мы с Вами проследим за тем, как неразгрызаемые неразрешимые орехи этого класса щелкал средневековый схоласт родом из захолустного Бетюна по имени Жан Буридан…

Тривиум отнюдь не тривиален. В частности, серьезного внимания заслуживает его интегральная часть под названием логика. Ни трепетное отношение к этой модели, ни попытки ее приодеть, а, скорее, раздеть на номиналистский вкус не были инновациями. Однако, умение разглядеть во внешности многократно запрещаемого к преподаванию радикального оккамизма новый широкий путь к светлому будущему – via moderna — многого стоило. Поставить многочисленные вопросы к общепринятому учебнику Петра Испанского и тщательно разобрать на них ответы. Написать комментарии настолько обширные, что они в несколько раз превысили объем изначального тернисто-терминистского опуса. Наконец, реабилитировать осужденную конкурсами средневековой красоты еретичку, заретушировав у нее на лице теологические морщины и вздыбив у нее на голове прическу в стиле томистского реализма. Казалось бы, эклектическая смесь двух конкурирующих менталок не может быть жизнеспособной. Но, если требуется вырезать из тела схоластического дискурса раковую опухоль избыточных сущностей, то зачем же сразу бритвой по горлу?! И в самом деле, в абстрактном философском смысле любое понятие нашего естественного ментального языка – результат работы многошагового алгоритма. Мы обнаруживаем в сенсорном хаосе мира формы определенных объектов, поскольку их сначала до нас доносит квантовая механика света, а затем для нас распознает зрительная система головного мозга. Мы расточительно развешиваем на окружающие предметы предикаты цвета, звука или запаха, не задумываясь о том, какую вычислительную цену за них заплатили. Соответствуют они один в один чему-то там, снаружи нас?! Можем ли мы, скажем, быть наивно уверенными в том, что пространство является тем самым картезианским ящиком, каковым мы себе его воображаем, а не чем-то виртуальным?! Пожалуй, все, что мы вправе утверждать, так это то, что наши ментальные модели полезны в целях выживания, а некоторые из них, может быть, лучше соответствуют реальному состоянию дел, чем другие. Примерно ту же доктрину, пусть и оставаясь на примитивно логическом уровне, защищал Буридан. Из истинности пропозиции «Сократ – богат» вовсе не следует наличие «богатства», — говорил он. Это всего лишь отношение между человеком и другими вещами, обычно именуемыми деньгами. Следовательно, древние древеса, представляющие подобного рода сущности, могут, если не должны быть безжалостно выкорчеваны из глухого бора неведения, оставляя место для культурных насаждений.

Квадривиум не только квадратура круга. В рамках этих четырех математических дисциплин можно задать бесконечное количество вопросов. В том числе тот, что остро заинтересовал Буридана в Questiones octavi libri physicorum – комментариях на восьмую книгу «Физики» Философа. Стрельба шла на поражение нашей хорошей знакомой – почитай, что самой плохой здоровьем модели Аристотеля: «движется ли снаряд, выпущенный рукой, при помощи воздуха? Если нет, то благодаря чему?» Но конкретно эта стрела направлялась не в теологическое молоко, как virtus derelicta Франциска из Марке, а норовила попасть точно в яблочко. Заметим вовне скобок – победный рост грядущих менталок динамики напрямую зависел от успешного выкорчевывания на делянке науки древних зарослей заблуждений. Аристотелевский воздух не в состоянии обтекать летящий снаряд и затем подпихивать его с тыла по ряду причин. Поставим, например, такой Gedanken- или самый настоящий experiment – запустим юлу. Даже закроем ее для верности в небольшом замкнутом пространстве какой-нибудь перегородкой. Очевидно, что она будет крутиться и после того, как мы отпустим от нее руку. Стало быть, дети обязаны продолжением своей забавы чему-то иному, нежели воздуху. Назовем эту штуку импетус. Что это такое? Осторожный магистр искусств искусно избегает ловушку врагов номинализма. Для него это некое вновь обретенное предметом «качество», а не реалистская акцидентальная форма. Обладает она и количественными атрибутами – при одинаковой скорости импетуса больше у тяжелого, т.е. более плотного при том же объеме тела. Да, он тоже заинтересован прикрутить к новорожденной модели как можно более привлекательных и полезных свойств. Как еще убедить современников ее полюбить?! Однако, в отличие от своих монашеских предшественников, он отказывается водрузить на голову хрупкой дамы груз постижения таинства Евхаристии. И причины угасания эха славословий Всевышнему в Эмпирее его тоже не интересуют. Впрочем, он тоже обращает свой ментальный взор ввысь и обнаруживает там хоровод небесных светил. Для его организации, по единодушному мнению Философа и Комментатора, необходимо было припахать на работу звездо-движителями команду интеллектуально одаренных персонажей, впоследствии идентифицированных христианами с ангелами. А ведь можно и сэкономить на их зарплате, если позволить Богу при сотворении мира снабдить планеты все тем же импетусом! Конечно же, не без благочестивого поклона в библейскую сторону: потому-то и сказано, что почил Он от всех дел Своих в день седьмый, впрочем, «я только попрошу господ богословов научить меня как это могло случиться».

Ткнул пальцем в небо, а получил прямое экспоненциально сложное попадание в искомую цель! Ведь, коль скоро хрустальные сферы все еще продолжают крутиться, подобно детской юле, стало быть, их импетус до сих пор не израсходован. У него нет срока годности! Но почему тогда на бренной Земле летящий снаряд в конечном итоге падает? А это от того, что он расходуется на преодоление сопротивления воздуха, который, следовательно, отнюдь не помогает, а мешает движению. Заключение совершенно правильное и диаметрально противоположное выводу, сделанному Франциском из Марке. Помимо того, отсюда недалеко до постулата единства законов природы подлунного и надлунного миров, ведь импетус и там наверху, и у нас внизу, тот же самый. Дух захватывает — количественные атрибуты оного предполагают наличие у небесных тел обыкновенной тяжести, объема и плотности. Так, может быть — страшно подумать! – Земля все-таки вертится?! Кажется невероятным, но эту безумную, чудну́ю модель уже в двадцатых годах 14-го столетия выдвигал оставшийся неизвестным герой, вероятнее всего, тоже какой-то парижский магистр свободных искусств. Увы, сорвать с нее смирительную рубашку правящей парадигмы науки, сдвинуть с мертвой точки юдоль печали простых смертных смелому опровержителю Аристотеля не удалось. Причины неудачи удачно объяснил Эдуард Ян Дяйкстерхаус: «Когда дело доходит до произведения заключения, Буридан, кажется, что больше подвержен влиянию Аристотелевской физики, нежели привлекательным упрощением картины мира, каковое позволила бы гипотеза вращения Земли, и потому продолжает в результате смотреть на Землю как на неподвижную массу в центре [Вселенной]. Его выбор полностью понятен: в те времена … речь шла не о деталях, но о вопросе, жестко связанным с основаниями Аристотелевской науки. Кто бы ни принял это решение и желал оставаться последовательным, был обязан отречься от всей натурфилософии и космологии, не имея возможности ничего предложить на их место. Какой-нибудь астроном мог позволить себе роскошество принять новую теорию, не заботясь о ее следствиях для принятых представлений о мире, ради того упрощения, что она предоставляла; от философа же, который должен был рассмотреть проблему в свете метафизики и позитивной науки нельзя было разумно ожидать, что он сделает такой шаг».

В одном замечательный голландский историк был неправ. Когда с высоты познаний третьего тысячелетия мы бросаем взгляд на первые детские шаги схоластов, то впадаем в грех т.н. NP-ляпа. Выдвижение адекватной гипотезы, в данном случае «привлекательного упрощения картины мира» только мерещится простой задачей в шаговой доступности — по той причине, что нам уже известен правильный ответ в конце учебника. На самом же деле, то был экспоненциально сложнейший гигантский прыжок через пропасть неведения, очередное чуднóе чудо…

И ожидать его осуществления измученному безнаучным прозябанием человечеству оставалось еще пара веков. Однако, конечно же, люди не сидели, сложа менталки. Руки моделей простираются к вам – в Блоге Георгия Борского.

Примечание: Модели, предложенные в целях концептуализации исторических событий и оценки деятельности исторических личностей, являются интеллектуальной собственностью автора и могут отличаться от общепринятой трактовки.