Вопросы, обнаружение феноменов, формирование понятий
Подробнее в статье: Фазы развития моделей
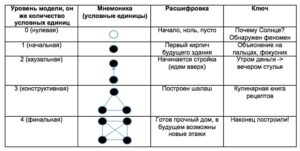

 0
0
Я запросто могу выразить семантику «извините» посредством «сорри» на руглише или «пардон» на фруссé, равно как и на нескольких других иноземных наречиях. Модели, соответствующие «замечательно», «чудненько» или «классно», отличаются друг от друга разве что где-то в высоких частотах культурно-образовательного спектра. Явление синонимии настолько общеизвестно и так прочно интегрировано в наш лексикон, что, казалось бы, не заслуживает внимания аналитической философии. Между тем, инопланетяне с астероида БГБ могли бы его разглядеть своим средним оком с помощью телескопа или даже без него – т.е. предсказать его наличие, не вникая в лингвистические особенности многочисленных земных языков. Дело не только и не столько в том, что слова – суть продукт совместного творчества множества независимых, но при этом ведущих схожий образ жизни сочинителей. Задача выживания в мире наподобие нашего сводится к произведению адекватных реакций на окружающий внешний или внутренний событийный поток. На практике у представителей homo sapiens эта немыслимо замысловатая деятельность разбивается на несколько этапов. На его нулевой фазе настоятельно необходимо расщепление общего гигантского домена феноменов на дискретный набор надежно распознаваемых ситуаций, с каждой из которых связана та или иная стратегия поведения. Эта операция в ее осознанном подмножестве производится комбинированием результатов работы отдельных подпрограмм, нарезающих сенсорный хаос на отдельные предикаты. Низлежащие под ними алгоритмы обязаны отвечать двум основным условиям – эффективности, сиречь, быстро вычисляться; и компактности — то бишь, быть малого размера (или, говоря математическим языком, обладать низкой Колмогоровской сложностью). Последний ингредиент критически необходим для их дальнейшей вербализации и передачи опыта ближнему своему. Так вот, эти-то два условия, взятые совместно, и означают, что когнитивная машинка в нашем распоряжении – аппарат весьма грубый, а нашинкованные ею куски с необходимостью будут слишком толстыми, т.е. произведенные понятия должны если не полностью копировать, то во многом пересекаться друг с другом…
Вышеупомянутая «стратегия поведения» – в общем случае суть тоже программа, определяющая наши действия. К тем из оных, что имеют осознанные модули-модели, тоже применимы аналогичные требования эффективности и компактности – мы ведь должны и уметь довольно быстро реагировать, и, пусть не спеша, подарить приобретенные навыки со знаниями подрастающему поколению. Посему нет ничего удивительного, что и в этой среде весьма распространена синонимия, правда, несколько другого рода – они похожи друг на друга вплоть до операции уподобления, чаще почти бесполезного метафорического, но иногда и полноценного математического. Хорошо известный нашим подписчикам со стажем тезис полиомии гласит, что любви все модели покорны – любая образованная из них супружеская пара может произвести хотя бы поэтически осмысленное потомство. Более знаменитый тезис, Черча-Тьюринга, также недоказанный и, по всей видимости, недоказуемый утверждает, что некие особи, особо богатые выразительными средствами и потому прозванные универсальными, могут приобрести себе все прочие вычислительные души, причем, на самых строгих законных основаниях. Помимо того, все они являются представителями одной и той же королевской фамилии, безраздельную власть которых над алгоритмическим пространством не смогут свергнуть самые Всемогущие небожители. Собственно, полупроводниковое воплощение одной из них прямо сейчас раздает многочисленные команды процессорам в том компьютере, что помогает вам читать эти строки. А вот обыкновенным нищим духом менталкам столь волшебные метаморфозы неподвластны. В некоторых случаях людям удается обнаружить, что между ними можно по всем инженерным правилам возвести мост, позволяющий перевезти груз проблем с одного берега ментальной реки на другой. Каждое такое событие достойно внимания средних глаз если не аналитических философов, то историков. И в особенности, коли оно произошло во столь же средние века и способствовало рождению науки…
Как-то раз после сытного ужина Николас Орем бросил обыкновенный взгляд на бурное море. И обнаружил ментальным зрением за Ла-Маншем Томаса Брадвардина и его команду оксфордских калькуляторов, безнадежно блуждавших в непроходимых дебрях слов и цифири своих опусов в нечеловеческих условиях туманного Альбиона. А затем обратил свой опять же мыслительный взор на университетскую Францию, овеваемую освежающим ветерком свободных искусств и залитую Солнечным светом демонстративных истин «Элементов» Евклида. И ему почему-то страшно захотелось состыковать эти божественно прекрасные модельные миры, разделенные беснующимися в волнах элементами, воедино. Если решение задачи о том, как посредством графической иллюстрации отобразить числа, было известно в далекой античности, то обратная операция казалась нетривиальной. Хуже того, ее полезность оспаривается даже в современности. Вот как живописал эту беду Маркус Джакинто: «В знаменитом тексте [от 1882 года], содержавшим первую строгую аксиоматизацию проективной геометрии, [Мориц] Паш написал: “теорема только тогда является воистину доказанной, когда ее демонстративное доказательство совершенно не зависело от иллюстраций”, тот же взгляд выразил [Давид] Гильберт в своем сочинении [от 1894 года] о фундаментальных основах геометрии. Отрицательное отношение к визуальному мышлению не ограничилось геометрией. Например, [Рихард] Дедекинд, поведал [в 1872 году] о [возникающем у него] непреодолимом чувстве неудовлетворенности при обращении к геометрической интуиции в базовом анализе бесконечно малых величин. Основания воспринимались неустойчивыми, а используемые понятия нечеткими и неясными. Как только таковые понятия были заменены точно определенными альтернативами без аллюзий к пространству, времени или движению, то оказывалось, что наши [предварительные, основанные на визуализации] интуитивные ожидания были обманчивыми, ненадежными [это подчеркивал Ханс Хан в 1933 году]. В некоторых кругах эта точка зрения превратилась в полное презрение к визуальному мышлению в математике: “В наилучших книгах”, – заявил [Бертран] Рассел [в 1901-м году], – нет совершенно никаких изображений”. Хотя некоторые математики, в частности [Феликс] Клейн [в 1893-м году], выражали несогласие с таким отношением, другие принимали его близко к сердцу. Скажем, [Эдмунд] Ландау, составивший [в 1934-м году] учебник по дифференциальному и интегральному исчислению, не использовал ни единой диаграммы». Воспользуемся синонимией и переведем этот пассаж на метафорический язык – на умопомрачительные модели глазеть следует не абы чем, а средним оком.
Нужен ли чудненько встроенный и замечательно работающий модуль визуального мышления классно развитой математике – сей вопрос остается философским и полемическим по сей день. Однако, не надо надевать очки на левое ухо, дабы уразуметь, что по отношению к четырнадцатому столетию задавать его было бы анахроничным. И тысячекратные «сорри» вперемешку с «пардон» вряд ли «извинили» бы вред, каковой бы нанес эмбриону науки тот недоброжелатель, что озадачил бы им Николаса Орема в его собственном веке. Тогда человечеству настоятельно надо было обнаружить как раз эту синонимию, дабы иметь возможность включить фонарь зрительной интуиции на скрывающемся во мраке пещеры неведения извилистом пути к дифференциальному и интегральному исчислению. Мы нынче полагаем, что окончательно расправился с этой задачей изобретатель аналитической геометрии, а заодно и современной философии Рене Декарт. На самом же деле первые бальные платья для сей модели, чтобы весело кружиться в Вальс-Комнате, пошил его схоластический предтеча-соотечественник. И вот каким образом это приключилось…
Дело было в неведомо каком году и сделано оно было в опусе, озаглавленном переписчиком «De latitudinibus formarum ab Oresme», каковое название я, сославшись на сложность нахождения в базе нынешних синонимов реликтовых предикатов, откажусь переводить со схоластического языка на руглиш, фруссé и все прочие известные мне наречия. Впрочем, от внимательных подписчиков не укроется тот факт, что я уже расписывался в своей лингвистической беспомощности по этому поводу в контексте Оксфордских калькуляторов. И впрямь, за отсутствием адекватных моделей нулевой фазы развития речь здесь идет о все той же белиберде. Аристотелевские формы, будучи напялены на материю, имеют ту или иную степень близости к совершенству, вот об этой-то штуке и пытались что-то промычать несчастные слово-лишенные средневековые титаны мысли при помощи чисел. Напомню, из того же Оксфорда происходило доказательство теоремы об «униформно деформированных» latitudinibus, каковая утверждала, что равномерное изменение какой-нибудь величины можно свести к постоянству ее среднего значения. Собственно, с этой точки и стартовало малое предприятие Орема по переселению арифметики в геометрию. А именно, он умудрился сообразить, что пресловутый «униформно деформированный» маразм может быть представлен в виде обыкновенного прямоугольного треугольника, а ее идентичность «недеформированному» собрату продемонстрирована посредством его сравнения с соответствующим усредненным прямоугольником. Это всего лишь взгляд на проблему самыми обычными очами с другой, визуальной стороны, но включившийся в работу могучий модуль зрительной интуиции понес орленка птенца Буриданова на своих крыльях значительно дальше. Что он, в принципе прекрасно осознавал и сам: «видимый пример быстро и совершенно захватывает воображение… поскольку иллюстрации помогают в познании самих вещей».
И тогда он с легкостью сгенерировал в своем внутреннем событийном потоке воображаемую трапецию, которая тоже могла представлять «униформно деформированную» величину, но не завершающуюся остроконечным круглым нулем. И ее насквозь беременную «округло деформированную» сестрицу. Наконец, произвольную кривую, изображавшую непонятно для чего нужную дикую «неуниформно деформированную» модель. Ба! – сообразил он, — да весь этот домен феноменов можно аккуратно нашинковать на ровным счетом 6 понятий – помимо двух благоразумно носящих униформу моделей, упомянутых в предыдущем абзаце, неплохо бы завести «выпукло» и «вогнуто» «разумные» дуги, а также все прочие «неразумные» особи непременно двух типов, опять же «выпуклые» и «вогнутые». Свою лучшую заявку на лавры изобретателя аналитической геометрии Николас Орем оставил, выразив на своем варварском схоластическом языке то, что можно было бы перевести как «уравнение прямой». Странное дело, зрительное мышление самыми банальными аппаратно-встроенными методами не подвело его, когда, рассмотрев со всех сторон двухмерный случай, он перешел к объемным фигурам, а следом уж к совершенно немыслимым четырехмерным пространствам…
Сдается мне, pace Мориц Паш, Давид Гильберт, Бертран Рассел, Рихард Дедекинд и иже с ними, что у их моделей даже не вооруженными телескопом глазами несложно распознать типичные симптомы миопии среднего ока. Как иначе интерпретировать тот факт, что они, замечательно различая самые тонкие детали в своей узкой специализации, не смогли увидеть более широкую панораму – не только средневековую, но и современную. Историки науки накопили множественные свидетельства того, когда редуцирование задачи синонимическим мостом к зрительно осязаемой проблеме приводило к решающему инсайту. Видеть значит ведать.
А ведать значит путешествовать по реке ИМ – Истории Моделей. Тем временем, наша зеленая стоянка на берегу Николаса Орема продолжается – в Блоге Георгия Борского.
 Примечание: Модели, предложенные в целях концептуализации исторических событий и оценки деятельности исторических личностей, являются интеллектуальной собственностью автора и могут отличаться от общепринятой трактовки.
Примечание: Модели, предложенные в целях концептуализации исторических событий и оценки деятельности исторических личностей, являются интеллектуальной собственностью автора и могут отличаться от общепринятой трактовки.
«Познай самого себя» — говорили мудрые древние греки, но и современные авторитеты нисколько не сомневаются, что они были правы.
Уважаемые читатели, дорогие друзья! Пара слов о самом себе. Без малого четверть века тому назад я покинул свою историческую родину, бывшую страну коммунистов и комсомольцев и будущую страну буржуев и богомольцев.
Ну вот, мы и снова вместе! Надеюсь, что Вы помните — в прошлый раз я определил тематику своего блога как «История моделей».