№397. Богатая модель

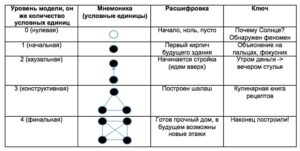
Когда-то на заре существования астероида БГБ я посчитал необходимым ввести в мир моделей кастовую структуру, распределив его обитательниц на несколько категорий. Величая же их «фазами», намекнул на то, что социальные лифты все-таки там функционируют исправно. Более того, по этой восходящей траектории проходит нормальный рост-житие сих прекрасных дам. Полагаю, что настало время освежить этот тезис в памяти подписчиков. За неимением времени и ограниченностью пропускной читательской способности не пойду экстенсивным путем, ограничившись интенсивными умозрительными соображениями. Итак, младенческая стадия новорожденных менталок – нулевая. Соответственно, им надо прежде всего научиться говорить, т.е. пополнить копилку человеческих понятий. Люди никогда не смогли бы первобытную голодную быль сделать сытой научной сказкой, кабы не имели в своем распоряжении по крайней мере пять хитроумных вычислительных подсистем, реализующих алгоритмы обнаружения в окружающем сенсорном хаосе полезные в целях выживания вещи. Более того, у этих устройств еще есть и гамма настраиваемых пользователем опций, при помощи которых можно практически бесконечно пополнять базу распознаваемых образов. Потому из этих кубиков можно строить и новые машины, чтобы потом быстро снимать с их выхода признак наличия тех или иных интересующих нас объектов – Сократа или Аристотеля, красоты или уродства. Несложно обнаруживать и отношения между ними – т.е. двух- и даже многоместные предикаты. Несколько парадоксален тот факт, что при этом на сенсорный вход сих черных ящиков не обязано хоть что-либо поступать. Скажем, перипатетики никогда не видели, не слышали и не чуяли ни единой субстанциальной или акцидентальной формы, равно как и никакой небесной кристаллической или земной элементной сферы. Они их выдумали, постулировали, то были продукты их здравого смысла и нездоровой фантазии. Однако, это нисколько не мешало им использовать их для описания практического любого явления природы.

Вот в этот-то момент, когда первые слова-понятия модель уже освоила, она может начать что-то с их помощью лепетать. Речь обычно идет о чукче-образном описании проплывающей перед глазами действительности. Эту фазу развития речи менталки я назвал начальной. Ее особенность заключается в иллюзии понимания, каковую я некогда проиллюстрировал при помощи метафоры фокусника. Происхождение всего, что угодно, случившегося в прошлом, может быть ею успешно «объяснено», а вот для того, чтобы сказать нечто содержательное о грядущем, менталке придется повзрослеть, перейдя в «каузальную» стадию. Зазубренные ею волшебные заклинания типа «если-то» позволяют людям вызывать всеведущих духов, способных сотворить для них те или иные предсказания. Впрочем, не все такие модели одинаково полезны. Только у самых ответственных особей со временем беззаботная юность остается позади, а их информационная полезность повышается до степени практической помощи обществу, когда из заданного идеального будущего они научаются вычислять способы его достижения. Тогда наступает пора «конструктивной» зрелости. Наконец, лишь некоторые избранные среди них могут с возрастом настолько преуспеть, что становятся способными объять своей, уже старческой, мудростью самые разнообразные вопросы из многочисленных областей знаний – тогда они вступают в счастливую «финальную» фазу жития, связанную не только со всенародной славой и почетными похоронами у нобелевской стены, но и со способностью выражаться замысловатым математическим языком.

Описав вышеописанную окружность, вернусь к самым нулевым истокам, босоногой и бесштанной фазе. И глубокомысленно отмечу, что понятия понятиям рознь. В частности, те из моделей, что берегут число смолоду, т.е. умеют «измерять» попадающий на их вход сигнал, выдавая цифирь в качестве результатов, имеют значительно больше шансов добраться до финального математического рая, являются дамами потенциально более общественно полезными и уже по факту весьма богатыми. Причина тому проста – при увеличении точности и разрядности измерения, они в состоянии предоставить нам в кредит практически неограниченное количество информации против единого бита «наличествует-нет» своих бедных булевских родственниц. Добавим к уже сказанному, что физический мир имеет странное пристрастие именно к математическим моделям, и мы выводим из этого их особое значение. Но как же их рожать, выкармливать и воспитывать? По мнению Годфри Харди для этого и делать-то особо ничего не надо: «Я сам всегда думал об ученом-математике в первую очередь как о наблюдателе, как о человеке, что всматривается в далекий горный хребет и записывает то, что обозрел. Его занятие состоит только в том, чтобы четко различить и поведать другим о наибольшем количестве разных вершин, каковые он смог разглядеть. Есть такие пики, что не сложно заметить, тогда как другие не столь ясны… Когда он обнаруживает один такой пик, то верит, что тот существует по той простой причине, что он его там видел. Если он хочет, чтобы кто-то другой тоже его узрел, то указывает на него напрямую или же через цепь вершин, заставившую его самого оный распознать. И когда его ученик тоже прозревает, то исследование, аргументация, доказательство завершены». Ага, держи глаза шире! Для начала нужно хотя бы посмотреть в правильную сторону. А если с подачи Аристотеля число превратилось в едва заметный сучок на дереве Порфирия?! А если нынешняя царица наук убирает золу на кухне тогдашней философии, в свою очередь работающей служанкой Госпожи Теологии?! Да и вообще, если в кромешном мраке темных веков ни зги не видно?! Для продвижения к свету знаний срочно требовался поворот в пифагорейско-платоновском направлении. Так вот, представьте себе — первые едва заметные контуры математического будущего обыкновенным комбинаторным чудом учуяли опять же схоласты четырнадцатого столетия христианской эры. И в их перипатетической труппе немаловажную роль сыграл все тот же магистр артистов Альберт Саксонский…

А сделать это было ох, как непросто. Посудите сами, какая каша варилась в котелках тогдашних мыслителей. В кладовке понятий Аристотеля наличествовали две модели нулевой фазы развития – количества и качества. Дамы не только различного характера, но и недолюбливающие друг друга. На выходе черного ящика первой из них появлялся сигнал при произведении элементарных арифметических операций — сложения или вычитания. Один человек — Сократ, второй — Платон, третьим будешь, Ксенофонт? Надо меньше пить! Ведь в ее ведении были еще и длины, площади или объемы, представлявшие собой тоже набор дискретных единиц. Тем самым, входить в отношения больше-меньше им было можно, но целая куча ничего принципиально нового против ее частей или элементов собой не представляла. Качествам же любое подобное кровосмешение было категорически запрещено, зато им разрешалось при некоторых условиях обладать различной интенсивностью. Скажем, если одно тело было горячее другого, то это от того, что ее соответствующая акцидентальная форма обладала повышенной интенсивностью теплоты, но ни в коем случае не повышенным количеством оной. Эту и без того печальную эпистемологическую ситуацию усугубляло желание схоластов применять перипатетическую понятийную базу для особо интересующих их теологических вопросов. Вот, скажем, один христианин – праведный, другой – еще более того, а третий и вовсе святой. Это как же следует понимать, то есть описать в терминах из учебника? Это у них количество праведности различное или качество другой категории? Сей заковыристый вопрос был успешно разрешен св. Фомой Аквинским в пользу последней опции. С ним повсеместно соглашались и многие другие. А Doctor Solemnus Генрих Гентский даже ввел по этому случаю в рацион средневекового питания новый понятийный ингредиент – latitudo formae. Дословно переводить этот маразм на русский язык не возьмусь, а вот семантику попробую растолковать. Каждая форма с его помощью получила свойство быть более или менее совершенной, находиться ближе или дальше от своего идеального состояния, иметь ту или иную интенсивность…

Возможно, наиболее революционным первым шагом Альберта Саксонского стал поворот шеи внимания к другим, далеким от богословия, материям. Ему, птенцу гнезда Буриданова, особенно приглянулась модель импетуса. Должно быть, потому все в тех же комментариях на «De Caelo et Mundo» он спросил сам себя: «Utrum omnis motus naturalis sit velocior in fine quam in principio?» — является ли естественное движение быстрее в конце, нежели в начале? Блиц-введение в тогдашний нулевой мир – естественным, в отличие от принужденного, Аристотель называл такое движение, которое происходит без какого-либо насильственного вмешательства. Это, например, когда камень падает на землю в контрасте с человеком, бросающим копье. Собственно, ответ на поставленный вопрос кажется очевидным любому младенцу, научившемуся подкидывать мячик вверх, но Истина, как известно, скрывается в деталях. Что это за штука такая, движение — качество или количество?! В первом случае менталка начальной фазы развития авторитетно лепечет что-то на своем вычурном языке, «объясняя» наблюдаемое явление природы посредством близости соответствующей акцидентальной формы к совершенному состоянию. По ее ученому мнению, ничего более информационного на эту тему и не скажешь. И только во втором, обретя доступ к числам, получает шансы сотворить нечто полезное для людей. Мы можем только догадываться, что побудило серьезного ученого сделать столь по-детски ошибочный, как с точки зрения аристотелевской науки, так и католической теологии, выбор. Трахнуло его по голове парой яблок, упавших с низкого и высокого дерева?! Или, побегав с кем-то наперегонки, он сообразил, что измерять преимущество победителя можно целым количеством корпусов между ним и побежденным? Или же захотел узнать, когда в точности его камень, брошенный в мысленно вырытый туннель, достигнет центра Вселенной?

Во всяком случае все тот же пресловутый латинский motus, пусть пока и только naturalis, для него теперь означал еще и нашу скорость. И он отчего-то страстно возжелал, если еще не количественно оценить эту штуку, порой потешно именуемую им интенсивностью движения, то выяснить по какому именно математическому закону она меняется в процессе падения. Непонятно, почему такой закон вообще должен существовать, тем паче математический?! Но он принимает это за аксиому и бесстрашно идет дальше. Растет скорость в арифметической или геометрической прогрессии? В зависимости от пройденного расстояния или времени? Несложно предложить бесконечное множество других возможных функциональных зависимостей?! Но что может быть совершеннее сих двух божественных моделей?! Все прочее не стоит и рассматривать! Впрочем, ограничив свой выбор четырьмя целями, Акелла Саксонский все равно умудрился промахнуться. Путем хитрых схоластических размышлений отверг все предложенные альтернативы, кроме одной. И получилось, как всегда. Стоило его грузу пролететь расстояние в два раза дальше, как его скорость удваивалась, в три – утраивалась и т.д.. Но разве эта ошибка была критической, имела существенное для рождения науки значение? Его далекие потомки, вооруженные механическими часами и наклонными плоскостями, научатся измерять скорость, проведут необходимые эксперименты и залатают мелкие дыры на украшенном формулами платье. По-настоящему же важным достижением средневекового философа было то, что он узрел на горизонте сознания далекие пики пифагорейско-платонического мира чисел. Мира не сакрального, но населенного информационно-богатыми детьми гор, строго необходимыми для воспитания менталок финальной фазы развития…

Мы уже провели достаточно времени в обществе холодных разумом континентальных мыслителей. Не рвануть ли нам на каникулы в самое пекло адски недружественных государств? Ладно ль моделям за морем, иль худо? Чудеса в свете Блога Георгия Борского продолжаются.

Примечание: Модели, предложенные в целях концептуализации исторических событий и оценки деятельности исторических личностей, являются интеллектуальной собственностью автора и могут отличаться от общепринятой трактовки.