№404. Галилейский рыбак

«Смилуйся, государыня рыбка! Что мне делать с проклятым народом?! Уж не хочет он жить будто в сказке. Хочет роботам быть владыкой. Чтоб они ему служили. У него на посылках чтоб были». Куды, о, куды бедному ученому податься?! Гранты на исследования выделяют богатые мира сего. А тем отвлеченные философские и, тем паче, математические соображения – не указ. Это люди практические, им прибыль да власть – вынимать да класть. Всех прочих заманивают рекламой – будете жить также хорошо, как никогда прежде! Ах, как бы дело не кончилось разбитым корытом… И проблема отнюдь не только в неумеренности людских желаний, но и в их несуразности. Лично я нисколько не боюсь страшилок о Всемогущем Искусственном Интеллекте, что, дескать, загонит обладателей естественного в клетки-землянки в homo-парках. Манипуляторы коротки! Да, мы уже научили железяки выкидывать различные хитроумные фокусы – например, бестолково болтать или ловко двигать фишками. Но для чуть ли не всех интересующих нас задач сложность имеет обыкновение расти по экспоненциальному графику. Потому подкрути разрядность входных данных, и самые производительные здоровяки-компутяги, напрасно колыхаясь всеми жабрами процессоров, утонут в бездонной пучине фазовых пространств. А вот с идейным планом дело обстоит значительно хуже. Я уж неоднократно бурчал на эту тему, но для пущего риторического эффекта повторюсь. Безраздельное господство физикалистских моделей приводит к тому, что мы воспринимаем себя самих как недоделанный эволюционный материал, как те же вычислительные машины, только белковые и маломощные. Соответственно, отрицая саму возможность вызова к себе в голову волшебных золотых мыслей, постепенно превращаемся в устройства ввода-вывода к кремниевым оракулам. Результаты сего печального превращения можно наблюдать на тех самых шахматах, что долгое время служили тестовым полигоном, где испытывалось и совершенствовалось лучшее оружие ИИ. Давно миновали те благословенные времена, когда великие гроссмейстеры разрабатывали нестандартные стратегические замыслы или оригинальные новые дебюты, когда зрительный зал, стоя, рукоплескал неожиданной прекрасной комбинации. Взрывное развитие компьютерных движков оставило за собой выжженную землю научной и творческой импотенции. Все, что осталось от некогда холеной королевской игры – выхолощенный спорт…

Метафорическая модель золотой рыбки поможет нам обратить внимание и на другую особенность человеческого когнитивного процесса – его цикличность, постоянное возращение к давно пройденным реперным точкам, к животворящим мертвечину застывших букв истокам. Старик в сказке Пушкина постоянно забрасывал свой невод, дабы выудить исполнительницу старушечьих чаяний. Подобно ему и масштабный ученый, коль скоро он желает сотрясти земную твердь существующей парадигмы, должен постоянно выглядывать из ящика «нормальной науки», высматривая в платоновских небесах вспышки сверхновых менталок. Так описывал процесс Артур Кёстлер: «Существует теория, предложенная Генрихом Сартоном и многими учеными считающаяся самоочевидной, которая говорит … что история науки суть единственная история, демонстрирующая кумулятивный прогресс [в деле обретения знаний]; что, соответственно, прогресс науки суть единственный способ измерить прогресс человечества; и что само слово ‘прогресс’ не имеет четко определенного значения в любой области деятельности – помимо научной… История науки демонстрирует рекуррентные циклы дифференциации и специализации, за коими следует реинтеграция на более высоком уровне… Этот процесс также имеет определенные аналогии с биологической эволюцией – такие, как расточительность [по отношению к ресурсам], внезапные мутации, борьба за существование между конкурирующими теориями». Собственно, обнаруженная известным писателем аналогия отнюдь неслучайна – оба эволюционных процесса, генов и мемов, являются примерами задачи поиска в экспоненциально-сложном фазовом пространстве. Ее невозможно решить без расточительности по отношению к ресурсам, без внезапных мутаций или борьбы за существование между конкурирующими теориями.

Более того, небесная обустроенность, то бишь дискретная математика, диктует свой безжалостный закон – в человеческих условиях наличия множества параллельно запущенных вычислительных процессов под названием «ученые», неизбежна и даже вероятна такая расточительность, что внезапно удачно мутировавшие, но нищие духом менталки погибнут в классовой борьбе с себе подобными богачами, не оставив здорового потомства. Если бы проводилось первенство мира по количеству мертворожденных моделей, то Николас Оремский был бы основным конкурентом на абсолютное первенство, причем, всех времен и народов. Мы уже познакомились с историями о том, как с его интеллектуального крючка сорвались золотые рыбки, способные превратить французского невезунчика в Коперника и Декарта. Сегодня же очередь не состояться Галилею… Как-то при случае, а именно во второй и третьей частях Мерлезонского балета, сиречь, трактата с прошлой лекции, он в очередной раз забросил сети в экспоненциальные глубины моря-окияна неведения. И вытащил было чудо-юдо-кита, на коем удалось бы разместить плодородную почву для произрастания по крайней мере полмира современной науки. И люди бы зажили также славно, как никогда раньше. И, несомненно, сложили бы иные сказки, воспевающие еще не старца-подкаблучника, а полного сил мужа, Галльского Галилейского рыбака…

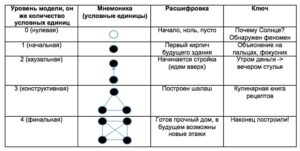
Собственно, на непосвященный взгляд интеллектуальное достижение Николаса выглядит весьма скромным – он всего лишь применил разработанную им же ранее математическую модель, предтечу аналитической геометрии, к определенной прикладной проблеме. Но какой проблеме! Не к тонкостям учета благотворительности, благодати или греховности — смертным грехам Оксфордских калькуляторов. А к тому самому обыкновенному движению, что так живо интересовало Жана Буридана и Альберта Саксонского. Его кривые, униформно, округло и неуниформно деформированные, теперь выправляли ошибки в понимании кинематики, графически представляя скорость. Но что это за штука такая, особенно в применении к неуловимому мгновению?! Палка-менталка, известная каждому ученику нынешней средней школы, была тщательно обстругана понятиями из схоластического словаря. Скажем, для тела в свободном падении она определялась пройденной за единицу времени дистанцией в предположении того, что более не изменится. Ну, а коль скоро это так, то соответствующие величины вполне можно было разместить на координатную плоскость. Более того, приняв те или иные стандарты, сопоставлять их значения, придать физический смысл осуществленным над ними арифметическим действиям. Но тогда не лишены семантики и геометрические фигуры, ограниченные с пола осью X, а сверху вышеупомянутым изогнутым небосводом! Скажем, их площадь в двухмерном или объем в трехмерном случае говорят нам что-то существенное. О чем именно говорят?! Сообразить это помогает вырожденный частный случай недеформированного движения. Это когда скорость постоянна и вместо потолка мы имеем идеальную выверенную по ватерпасу горизонтальную прямую. Тогда налицо картинка прямоугольника, и очевидно, что произведение смежных сторон оного содержит некую релевантную информацию о пройденном пути. Но останется ли это забавное наблюдение за природой вещей верным для общего кривого случая или хотя бы некоторых его разновидностей?!

Здесь-то и проявился научный гений искусного ловца модельных душ. Какой же русский не любит быстрых выводов?! А Вы думаете французы – ой-ля-ля! – в этом отношении не тем лыком шиты?! Разве что те из них, кто знает толк в математике. И Николас Орем оказался как раз представителем этого странного подвида homo sapiens. Он выбирал свой невод крайне осторожно, вкрадчиво продвигаясь вперед крошечными ментальными шажками. Для начала распилил свой график по всей длине на модные в схоластическом дискурсе т.н. пропорциональные части. Сперва надвое, потом правый кусок хрусть, и еще раз пополам и т.д. – так, что получились 1/2, 1/4, 1/8 от целого и так далее, до тех пор, пока уж сам черт черту не прочертит. А затем приколотил на каждую все более тонкую вертикальную балку горизонтальные перекладины, причем, так, чтобы высота их линейно возрастала – 1, 2, 3… На произвольном из нарезанных участков площадь прямоугольника вычислялась по банальному алгоритму из предыдущего абзаца, но какова общая сумма материала, ушедшего на строительство всей лестницы?! Ровным счетом 2 единицы или вчетверо больше первого фрагмента – истинность этой простой теоремы удалось продемонстрировать строгим дедуктивным образом. За первым ходом последовал следующий, не менее аккуратно просчитанный. Что, если соорудить на том же самом месте вместо ступенек гладкую треугольную горку, представляющую тем самым «униформно деформированную» величину?! И здесь точный подсчет затрат не вызвал ни малейших затруднений. Познания в «Элементах» Евклида помогли получить искомый результат – и эта задача элементарно сводилась к недеформированному варианту. Наконец, пришел черед решать и более заковыристые комбинированные задачки. Пускай на первой пропорциональной части амплитуда по оси Y – величина постоянная, равная единице. На второй позволим ей линейно добраться до двойки. Затем на третьей снова усмирим ее аппетиты к росту. Зато на четвертом отрезке отпустим добежать до 4-ки и т.д. Какие средства придется потратить на строительство?!

Оставлю этот блеклый математическо-схоластический вопрос прозябать в виде домашнего задания, а сам воспарю в лазурные платоновские небеса. Несложно подметить, что Николас был весьма близок к изобретению интегрального и дифференциального исчисления. Не хватило самого малого – понятия малых, причем, бесконечно, величин. Еще ближе подошел он к открытию закона движения тел в свободном падении – не то, что рукой, а и языком подать можно, так горячо. Собственно, все, что оставалось сделать, это поставить свою модель рядышком с подружкой, хоть и спекулятивной, но продвигаемой его ближайшим коллегой по буриданизму Альбертом Саксонским. Тот в одном из своих опусов осмелился предположить, что скорость устремившегося к месту постоянной прописки аристотелевского камня менялась как раз по униформно-деформированному правилу – т.е. имела постоянное ускорение. Все эти менталки потенциально могли попасть в голову Орема при условии удачной рыбалки. Однако, дело пошло не шатко и не валко. Должно быть, что-то фундаментально неправильное вымаливала бабка его времен, олицетворявшая кумулятивные народные чаяния. Многие, очень многие люди вожделели не жить лучше, а умереть за Царя Небесного, не любить ближнего своего, а уничтожать инакомыслящих, не защиты мира, а захватнической войны. Потому-то золотая рыбка игриво вильнула хвостиком и, раздраженная не столько неумеренными, как несуразными человеческими желаниями, скрылась в глубинах моря-окияна неведения. Галилейский рыбак как был, так и остался бедняк, не сумев стяжать лавров Галилео. И его духовные дочери, клинически нищие духом, сгинули в классовой борьбе с себе подобными богачами, не оставив здорового потомства. И средневековый люд стал жить-поживать также хорошо, как современный россиянин после череды блистательных побед бункерного деда. В старой землянке у разбитого корыта…

Даешь каждому печальному финалу свой жизнеутверждающий сиквел! По крайней мере, мы, в отличие от роботов, несмотря на экспоненциальную сложность задачи, имеем шансы отловить невынужденные ошибки и сделать из них адекватные выводы. Нырнем в водоворот веков – с Блогом Георгия Борского.

Примечание: Модели, предложенные в целях концептуализации исторических событий и оценки деятельности исторических личностей, являются интеллектуальной собственностью автора и могут отличаться от общепринятой трактовки.